引言

在讨论本文的中心问题之前，我想先要讨论一下电感和电容的相关特性：

首先是电感：

我们知道，一个线圈就是一个比较简单的电感，而电感有一个特点：当磁场变化时，线圈为了消除磁场变化而使自身产生感应电压，这对应法拉第电磁感应定律：

e=\frac{\Delta\phi}{\Delta t}

\phi=LI ，其中 e 表示感应电动势， t 表示时间， \phi 表示磁通量， L 表示电感大小， I 表示电流大小。
我们将上式进行变形，令 V_L 表示该电感产生的电动势，则：

V_L=L\times\frac{\Delta i}{\Delta t}

化为微分形式就是：

V_L = L\times \frac{di}{dt}

然后是电容：

我们知道： Q=CE ，其中 Q 表示电容内的电荷， C 表示电容大小， V 表示电容两端的电位差，同时我们知道： Q=It ，因此我们设 I_C 表示通过该电容的电流，则：

I_C=C\times \frac{\Delta V}{\Delta t}

化为微分形式就是：

I_C=C\times \frac{dV}{dt}

正文

接下来，我们首先了解一下复数的基本知识：

在直角坐标系下，复数定义为： a+bj ，其中 j^2=-1 ， a 称为实部， b 称为虚部

在复数中有一个非常著名的公式叫做欧拉公式：

e^{j\theta}=cos\theta+jsin\theta ，一个简单的证明如下：

对等式左侧进行Maclaurin展开：

e^{j\theta}=1+\frac{j\theta}{1!}+\frac{(j\theta)^2}{2!}+\frac{(j\theta)^3}{3!}+\frac{(j\theta)^4}{4!}+\frac{(j\theta)^5}{5!}+\frac{(j\theta)^6}{6!}+\frac{(j\theta)^7}{7!}+...

利用 j^2=-1 这一性质，上式可化为：

e^{j\theta}=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}...+j(\frac{\theta}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}...)

而

cos\theta=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}...

sin\theta=\frac{\theta}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}...
因此欧拉公式得证

可以注意到，一个复数 z=a+bi ，若将 a 作为直角坐标系的横轴， b 作为直角坐标系的纵轴，那么一个复数可以表示为直角坐标系上的一个向量 (a,b) ，其与 a 正半轴的夹角叫做复数的幅角，若设复数的幅角为 \theta ，则 tan\theta=\frac{b}{a}

我们将复数 z 变换到极坐标系上：

已知：

a=|z|cos\theta
b=|z|sin\theta

z=\sqrt{a^2+b^2} （这定义为复数的模，或者说是复数在平面直角坐标系上表示时的长度）

那么利用欧拉公式可得： z=a+jb=|z|cos\theta+|z|jsin\theta=|z|e^{j\theta}

我们平常使用的交流电可以定义为： V=V_{m}sin(\omega t+\varphi)

其中 \omega 表示角频率， \varphi 表示初始相角

对于下述电路：

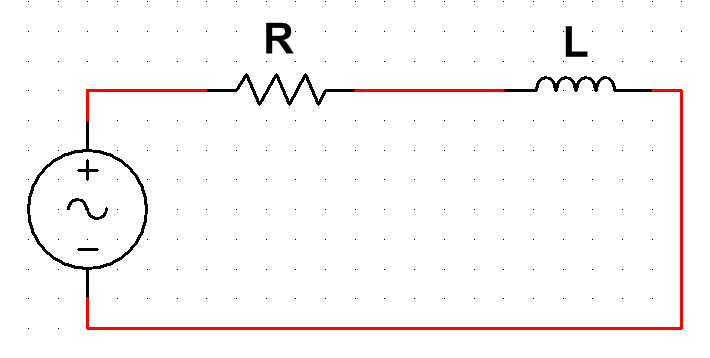
我们根据上面的讨论，很容易列出下列等式：

Ri+L\frac{di}{dt}=V_{m}sin(\omega t+\varphi)

其中电流 i 是关于时间 t 的函数，求解这个方程需要用到高等数学微分方程部分的知识，且求解过程非常复杂。

但是我们可以利用复数轻松求解这个问题：

首先让我们转换一下思想，我们知道一个交流电源包含幅度、角频率及初始相位三个参数，那么我们完全可以用复数的模来表示幅度，复数的幅角来表示角频率及初始相位，因此交流电源电压描述可以变为如下表达式：

\dot{V}=a+bj ，其中 |\dot{V}|=\sqrt{a^2+b^2}=V_{m} ，幅角 \theta=\omega t+\varphi ，

根据上述讨论的复数在极坐标下的定义，可以将该表达式改写为：

\dot{V}=V_{m}e^{j(\omega t+\varphi)}=V_mcos(\omega t+\varphi)+jV_msin(\omega t+\varphi)

我们知道上述方程的解一定也是同角频率正弦波（参考高等数学相关微分方程的求解），因此电流类似的改写为：

\dot{I}=I_{m}e^{j(\omega t+\varphi_2)}=I_mcos(\omega t+\varphi)+jI_msin(\omega t+\varphi_2)

因此上述微分方程可以简化为：

R\dot{I}+L\frac{d\dot{I}}{dt}=\dot{V}

由于我们只是改变了电压的描述形式，并规定了电流函数解的形式，因此这样代入并不改变上述方程的成立性

我们继续化简：

\frac{d\dot{I}}{dt}=\frac{d(I_me^{j(\omega t+\varphi_2)})}{dt}=I_me^{j\varphi_2}\frac{d(e^{j\omega t})}{dt}=I_me^{j\varphi_2}j\omega e^{j\omega t}=j\omega I_me^{j(\omega t+\varphi_2)}=j\omega \dot{I}

因此上述方程化简为：

R\dot{I}+j\omega L\dot{I}=\dot{V}

这就是一个简单的代数方程式，而求解该方程中的 \dot{I} 的方法我们小学四年级就已经学过了：

\dot{I}=\frac{\dot{V}}{R+j\omega L}

同时，我们已知在仅含有电阻 R 直流电路中，依据欧姆定律可得： R=\frac{V}{I} ，其中 V 为电阻两端的电压， I 为电阻两端的电流

类似的，我们在交流电路中引出阻抗的概念，定义为： Z=\frac{\dot{V}}{\dot{I}}

因此，根据上述计算，我们可以很容易得出，电感的感抗为： \dot{Z_L}=\frac{j\omega L\dot{I}}{\dot{I}}=j\omega L

类似的，电容的容抗为： \dot{Z_C}=\frac{1}{j\omega C}=-j\frac{1}{\omega C}

电阻的阻抗为： \dot{Z_R}=R

我们称上面带点的符号为相量，相量具有幅度和相位两个参数，利用相量，我们可以判断交流回路中电压和电流的相位差借此判断相位的超前与滞后现象